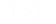Image Transormations
Geometric transformations
- Geometric transforms permit the elimination of geometric distortion that
occurs when an image is captured. Geometric transforms can also be used to
preform a desired geometric distortion.
- Example: The attempt to match remotely sensed images of the same area taken after one year, when the more recent image was probably not taken from precisely the same position.To inspect changes over the year, it is necessary first to execute a geometric transformation, and then subtract one image from the other.
- A geometric transform is a vector function T that maps the pixel (x,y) to
a new position (x',y').
![]()
- The transformation equations are either known in advance or can be determined from known original and transformed images.
- Several pixels in both images with known correspondence are used to derive the unknown transformation.
A geometric transform consists of:
- Determine the Pixel Co-ordinate Transformation
- mapping of the co-ordinates of the input image pixel to the point in the output image.
- the output point co-ordinates should be computed as continuous values (real numbers) as the position does not necessarily match the digital grid after the transform.
- Find the point in the image which matches the transformed point and
determine its brightness.
- brightness is typically computed as an interpolation of the brightnesses
of several points in the neighborhood.
- brightness is typically computed as an interpolation of the brightnesses
of several points in the neighborhood.
Pixel co-ordinate transformations
- General case of finding the co-ordinates of a point in the output image
after a geometric transform.
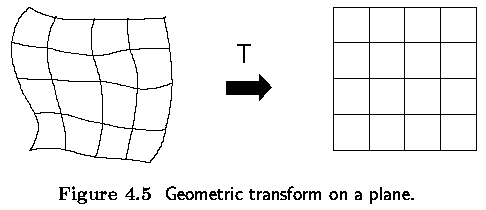
- usually approximated by a polynomial equation
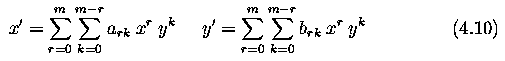
- This transform is linear with respect to the coefficients ark, brk
- If pairs of corresponding points (x,y), (x',y') in both images are known, it is possible to determine ark, brk by solving a set of linear equations.
- More points than coefficients are usually used to get robustness.
- If the geometric transform does not change rapidly depending on position in the image, low order approximating polynomials, m=2 or m=3, are used, needing at least 6 or 10 pairs of corresponding points.
- The corresponding points should be distributed in the image in a way that can express the geometric transformation - usually they are spread uniformly.
- The higher the degree of the approximating polynomial, the more sensitive to the distribution of the pairs of corresponding points the geometric transform.
Bilinear Transformation
- In practice, the geometric transform is often approximated by the
bilinear transformation
- 4 pairs of corresponding points are sufficient to find transformation coefficients
| In-Class Assignment/Exercise Create a set of 20 images that will be used to make up a video sequence. 1) Write a program to has an option to display the 20 images in a loop like a looped video sequence. 2) Perform Decimation on this Sequence in the time domain (down-sample in the time domain) and reduce the number of frames by 10. This is a crude way of performing a form of compression....you are reducing the number of frames. How would you do this? Would you discard every other image in your video sequence? Make this an option in your program and display the results? What does this look like....what has happened? 3)Now perform Interpolation on the decimated video sequence. This will show you how after our simple compression in step 2 we can try to improve the results when played back to the user. Interpolation will now take place in the time domain. We have already seen how to decimate and interpolate in the spatial domain; this extends very naturally to decimating and interpolating in the time domain (decimating and interpolating the image frames). To do this, use a bilinear interpolation scheme to interpolate in between frames. For example, to interpolate the frame between frame1 and frame2, you will be using a triangular kernel centered at frames 1 and 2 at each pixel (this should actually be pretty easy since you are only interpolating by a factor of 2). Display the reinterpolated image sequence and comment on how it compares to the original video sequence. |
Affine Transformation
- Even simpler is the affine transformation for which three pairs of corresponding points are sufficient to find the coefficients

- The affine transformation includes typical geometric transformations such
as
- rotation, translation, scaling and skewing.
- A geometric transform applied to the whole image may change the co-ordinate system, and a Jacobean J provides information about how the co-ordinate system changes
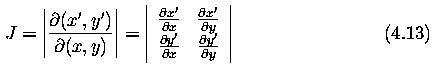
- If the transformation is singular (has no inverse) then J=0. If the area of the image is invariant under the transformation then J=1.
- The Jacobean for the general bilinear transform (4.11)
![]()
- The Jacobean for the affine transformation (4.12)
![]()
Important geometric transformations
- Rotation - by the angle phi about the origin
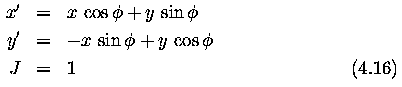
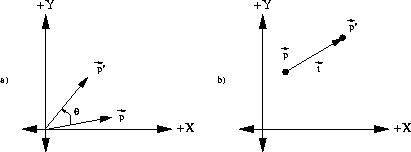
Figure: (a)Anticlockwise rotation of point p by angle theta, (b) Translation of the point p by the vector t - Change of scale - a in the x axis and b in the y axis

- Skewing by the angle phi
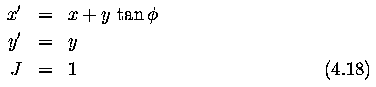
Write a program that rotates an image by a specified angle. The
transformation for rotation by angle t around point (xc, yc) is x' = (x - xc) cos t - (y - yc) sin t + xc y' = (x - xc) sin t + (y - yc) cos t + ycApply your method to the image in 15 degree increments to rotate the image by 120 degrees. Compare this to rotating directly by 120 degrees. What happens? Why? |
Complex geometric transformations (distortion)
- approximation by partitioning an image into smaller rectangular subimages;
- for each subimage, a simple geometric transformation, such as the affine, is estimated using pairs of corresponding pixels.
- geometric transformation (distortion) is then performed separately in each subimage.
- Typical geometric distortions which have to be overcome in remote sensing:
- distortion of the optical systems
- nonlinearities in row by row scanning
- nonconstant sampling period.
- Assume that the planar transformation has been accomplished, and new point co-ordinates (x',y') were obtained.
- The position of the point does not in general fit the discrete raster of the output image.
- Values on the integer grid are needed.
- Each pixel value in the output image raster can be obtained by brightness interpolation of some neighboring noninteger samples.
- The brightness interpolation problem is usually expressed in a dual way (by determining the brightness of the original point in the input image that corresponds to the point in the output image lying on the discrete raster).
- Computing the brightness value of the pixel (x',y') in the output image
where x' and y' lie on the discrete raster

- In general the real co-ordinates after inverse transformation (dashed lines in Figures) do not fit the input image discrete raster (solid lines), and so brightness is not known.
- To get the brightness value of the point (x,y) the input image is
resampled.
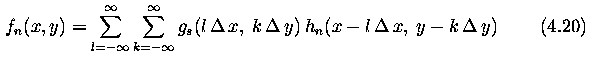
- f_{n}(x,y) ... result of interpolation
- h_{n} is the interpolation kernel
- Usually, a small neighborhood is used, outside which h_{n} is zero.
Nearest neighbor interpolation
- assigns to the point (x,y) the brightness value of the nearest point g in
the discrete raster
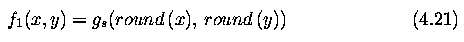
- The right side of Figure shows how the new brightness is assigned.
- Dashed lines show how the inverse planar transformation maps the raster of
the output image into the input image - full lines show the raster of the
input image.
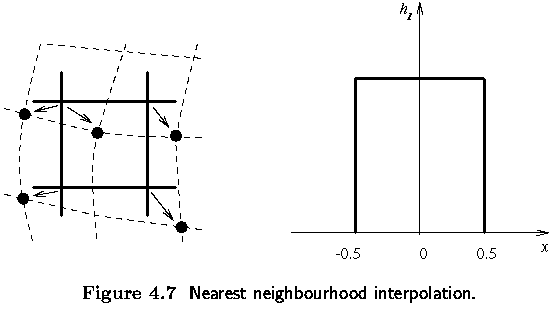
- The position error of the nearest neighborhood interpolation is at most half a pixel.
- This error is perceptible on objects with straight line boundaries that may appear step-like after the transformation.
Linear interpolation
- explores four points neighboring the point (x,y), and assumes that the
brightness function is linear in this neighborhood.
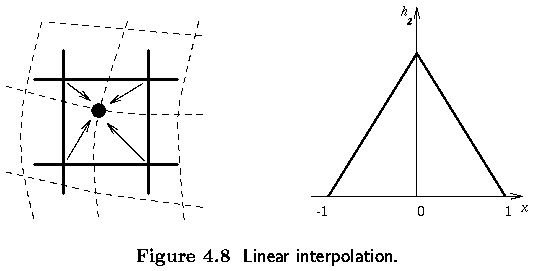
- Linear interpolation is given by the equation
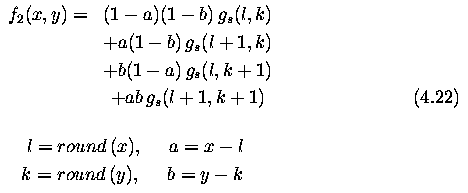
- Linear interpolation can cause a small decrease in resolution and blurring due to its averaging nature.
- The problem of step like straight boundaries with the nearest
neighborhood interpolation is reduced.
Bicubic interpolation
- improves the model of the brightness function by approximating it locally by a bicubic polynomial surface; sixteen neighboring points are used for interpolation.
- interpolation kernel (`Mexican hat') is given by
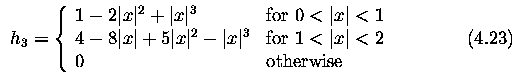
- Bicubic interpolation does not suffer from the step-like boundary problem of nearest neighborhood interpolation, and copes with linear interpolation blurring as well.
- Bicubic interpolation is often used in raster displays that enable zooming with respect to an arbitrary point -- if the nearest neighborhood method were used, areas of the same brightness would increase.
- Bicubic interpolation preserves fine details in the image very
well.