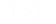Learning Algorithms (optimizers)- Another Factor Influencing Training

 

There are different gradient descent algorithms that are in use in Machine Learning. The goal of these algorithms is to attemp to when reducing loss get out of local minimum and find a good solution (ideally the best). This is an "optimization problem" and there are many algorithms developed to solve it. Here are a few that are commonly used.

The following is taken and modified from " A Visual Explanation of Gradient Descent Methods (Momentum, AdaGrad, RMSProp, Adam) "

Plain Gradient Descent

The basic gradient descent algorithm follows the idea that the opposite direction of the gradient points to where the lower area is. So it iteratively takes steps in the opposite directions of the gradients. For each parameter theta (weight in the network), it does the following. This works fine if your starting point is in the valley of the global minimum.

delta = - learning_rate * gradient

theta += delta

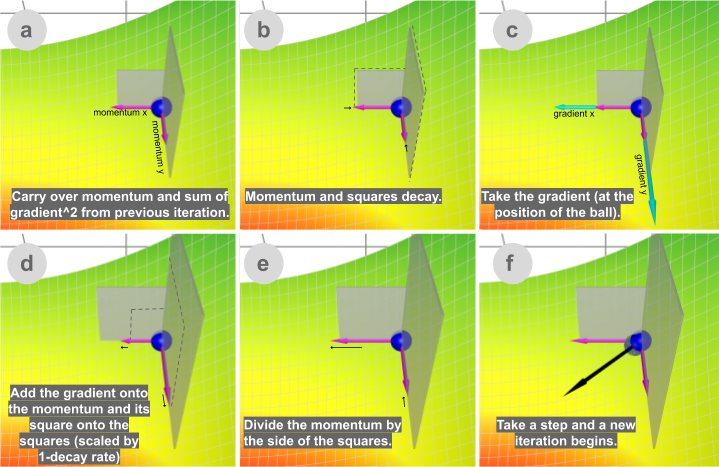
Momentum

 

The gradient descent with momentum algorithm (or Momentum for short) borrows the idea from physics. Imagine rolling down a ball inside of a frictionless bowl. Instead of stopping at the bottom, the momentum it has accumulated pushes it forward, and the ball keeps rolling back and forth. Here is an illustration of the idea

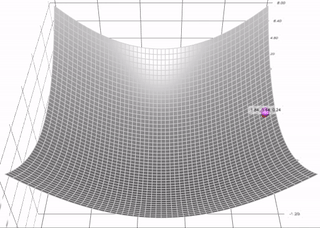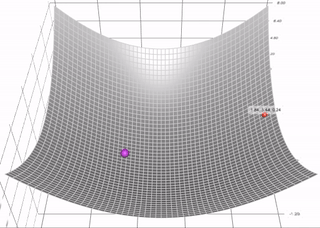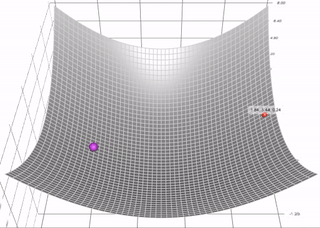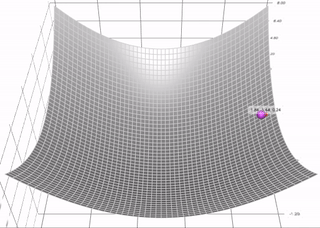
We can apply the concept of momentum to our vanilla gradient descent algorithm. In each step, in addition to the regular gradient, it also adds on the movement from the previous step. Mathematically, it is commonly expressed as:

delta = - learning_rate * gradient + previous_delta * decay_rate (eq. 1)

theta += delta (eq. 2)

This can be rewriten as :

sum_of_gradient = gradient + previous_sum_of_gradient * decay_rate (eq. 3)

delta = -learning_rate * sum_of_gradient (eq. 4)

theta += delta (eq. 5)

 

Comparing Plain Gradient Descent & Momentum

 

 

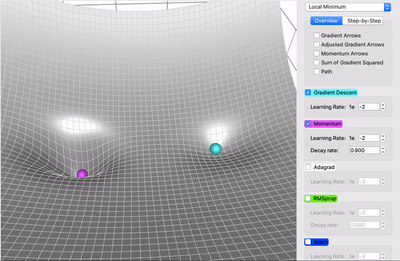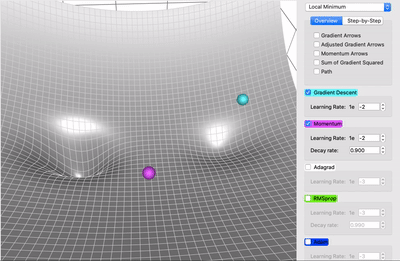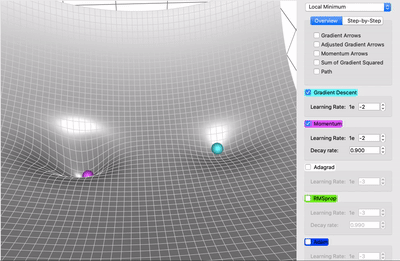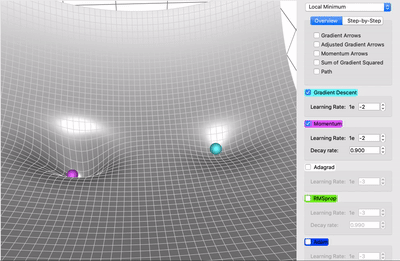
AdaGrad

Instead of keeping track of the sum of gradient like momentum, the Adaptive Gradient algorithm, or AdaGrad for short, keeps track of the sum of gradient squared and uses that to adapt the gradient in different directions. Often the equations are expressed in tensors. I will avoid tensors to simplify the language here. For each dimension:

sum_of_gradient_squared = previous_sum_of_gradient_squared + gradient²

delta = -learning_rate * gradient / sqrt(sum_of_gradient_squared)

theta += delta

 

Comparison of gradient descent and AdaGrad

 

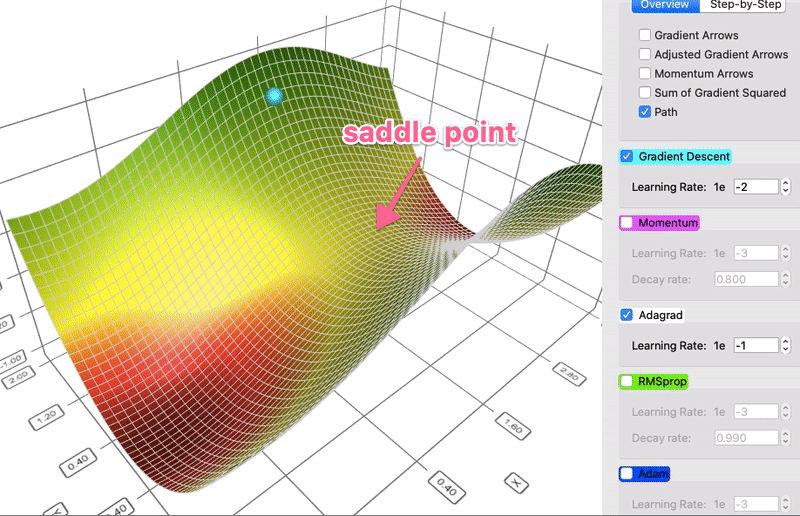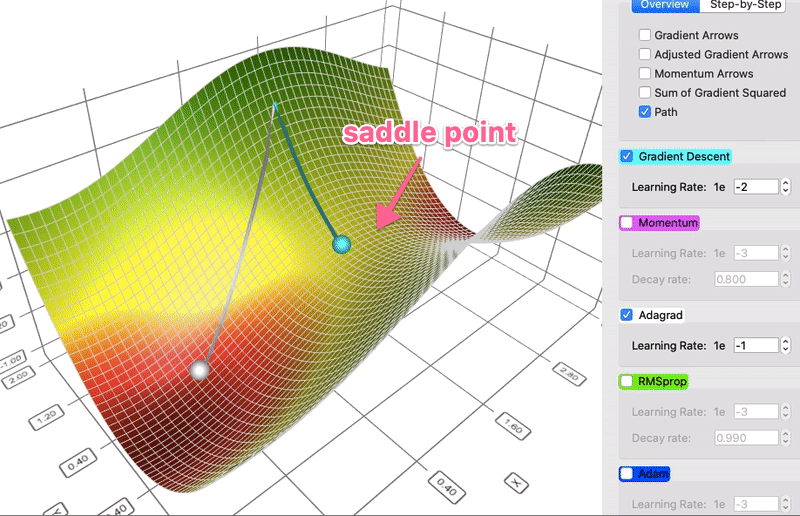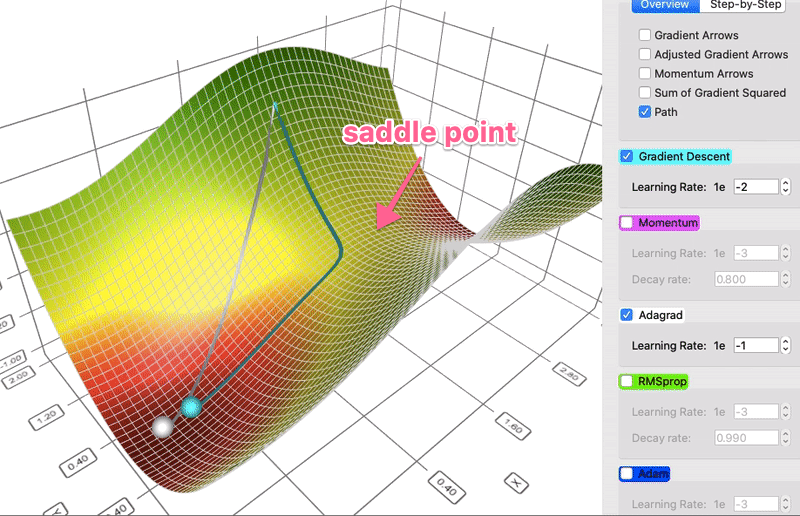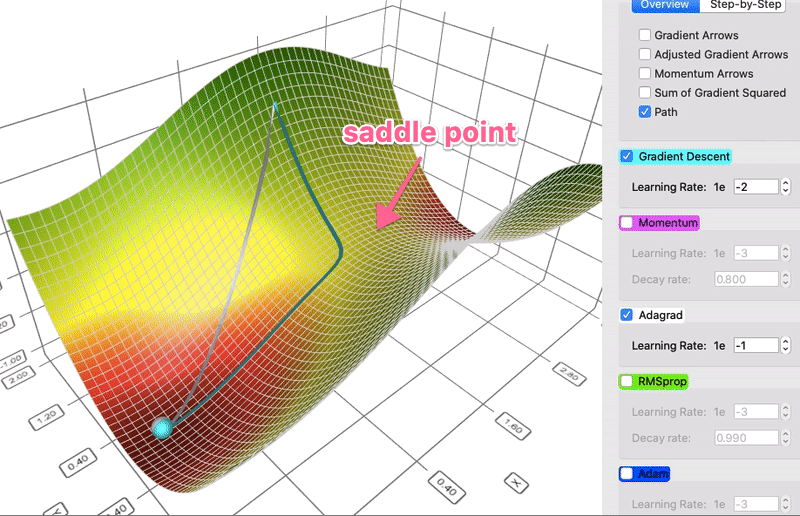
RMSProp

AdaGrad t is slow. This is because the sum of gradient squared only grows and never shrinks. RMSProp (for Root Mean Square Propagation) fixes this issue by adding a decay factor.

sum_of_gradient_squared = previous_sum_of_gradient_squared * decay_rate+ gradient² * (1- decay_rate)

delta = -learning_rate * gradient / sqrt(sum_of_gradient_squared)

theta += delta

 

Comparing AdaGrad and RMSProps

 

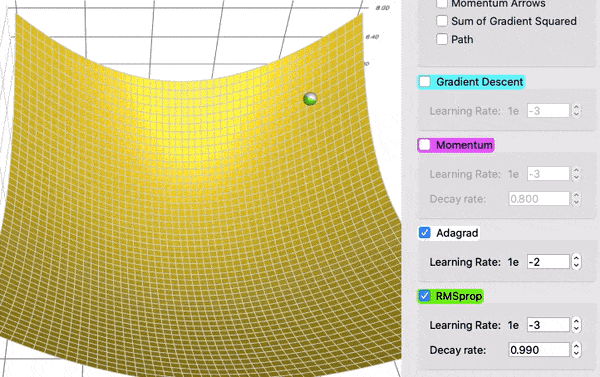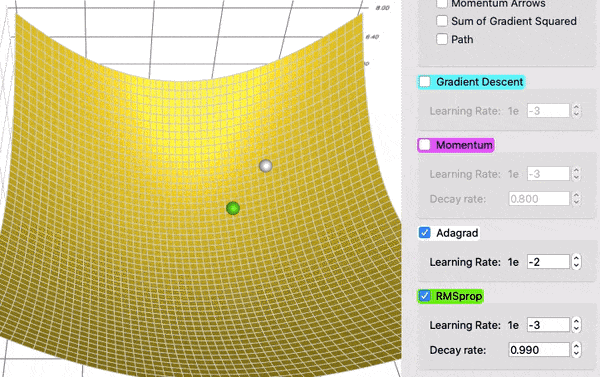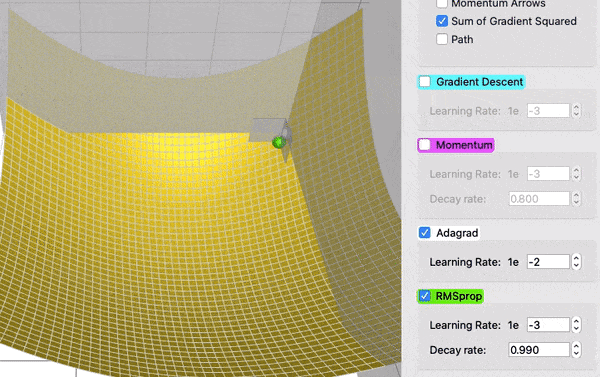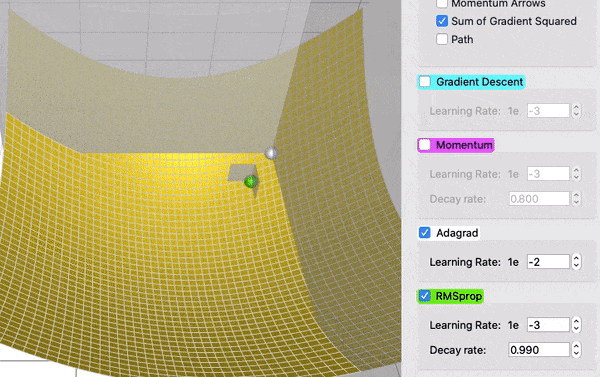
Adam

 

Adaptive Moment Estimation) takes the best of both worlds of Momentum and RMSProp. Adam empirically works well, and thus in recent years, it is commonly the go-to choice of deep learning problems.

Let’s take a look at how it works:

sum_of_gradient = previous_sum_of_gradient * beta1 + gradient * (1 - beta1) [Momentum]

sum_of_gradient_squared = previous_sum_of_gradient_squared * beta2 + gradient² * (1- beta2) [RMSProp]

delta = -learning_rate * sum_of_gradient / sqrt(sum_of_gradient_squared)

theta += delta

 

Beta1 is the decay rate for the first moment, sum of gradient (aka momentum), commonly set at 0.9.

Beta 2 is the decay rate for the second moment, sum of gradient squared, and it is commonly set at 0.999.

Adam gets the speed from momentum and the ability to adapt gradients in different directions from RMSProp. The combination of the two makes it powerful.